노션에 정리한 걸 티스토리에도 올리고자 한다
노션 => 티스토리로 옮기면서 빠지는 내용이 있으니
노션게시물을 따로 올리면, 그걸 함께 보시는 걸 추천드립니다
[CS22SN] 우리는 왜 NLP가 필요할까? / Lecture 1 - Intro & Word Vectors | Notion
인간의 언어는 다양한 의미를 가지고 있기 때문에 이를 처리하는 NLP 과정이 필요하다.
spiky-cadet-06f.notion.site
그냥 드래그해서 긁어오니 하얗게 배경이 생겨서 이상하다 ㅠㅠ 왤까...

인간의 언어는 다양한 의미를 가지고 있기 때문에 이를 처리하는 NLP 과정이 필요하다.
word2vec
- 언어는 사람들이 구성하는 해석하는 사회적 시스템 => 그러나 컴퓨터가 이해하기 힘듬
- 언어는 공식적인 체계가 아님 => 어떤 영향을 미치는지 잘 추측해야함
- 언어는 최근에 만들어짐, 엄청난 힘을 가짐
인공지능은 인간의 지식을 필요하고 인간도 인공지능이랑 대화를 해야됨~
이 cycle을 어떻게 구축할까
인간-컴퓨터 사이의 사이클 구축하는 방법
- 신경학적 방법
- 기계 학습
- NLP는 GPT로 인해 기술이 바뀌었음
전통적으로 실제 언어 처리시스템
단어사전(word net) 는 이산 기호로 만듬

Logistic Regression(로지스틱 회귀)란?
Logistic 는 sigmoid 함수라고도 하며, 입력을 0 - 1 사이의 값으로 매핑하여 종속 변수가 1의 값을 취할 확률을 구하는 것
Logistic Regression 는 true, false 두 가지 상황을 표현하기 위해 사용
- 직선을 사용하면 제대로 표현이 안됨
- Logistic Regression는 이진 분류(binary classification) 문제를 해결하기 위한 통계적 방법
Logistic Regression는 독립 변수들의 선형 결합을 사용하여 종속 변수의 확률을 예측.
- 종속 변수는 두 개의 범주 중 하나를 가질 수 있는 이산 변수 ( true, false)
- 만약 Logistic Regression 모델을 만들고 있다면, 모텔과 호텔을 나타내는 one- hot 레코딩으로 만들 수 있음
motel = [0000000001000]
hotel = [0000100000000]
Logistic Regression 문제점
- 모든 단어를 만들려면, 5백만 벡터가 필요
- 호텔 모텔처럼 유사한 의미지만 벡터에서 유사도가 없음
해결방법
distributional sematics 분산적 의미론
- (얼마나 자주 등장하는가? 어떤 맥락에서 등장하는가?)
ex) 은행이 발생하는 여러 곳을 찾고 근처의 단어들을 컨텍스트 단어로 모음
은행을 둘러싼 단어들이 어떤 의미에서 은행이라는 단어의 의미를 나타낼것이라고 본다 .
자연어처리에서 단어와 토큰을 사용
word embeddings
- 문맥에서 발생하는 단어로 보는 것
- 단어에 대한 실제값 벡터는 벡터가 문맥에서 나타는 다른 단어를 예측하는데 유용함
왜 임베딩이라고 하나요?
단어 전체를 가질 때, 단어들을 모두 고차원 벡터 공간에 위치시키고 그 공간에 임베딩됨
Word2vec
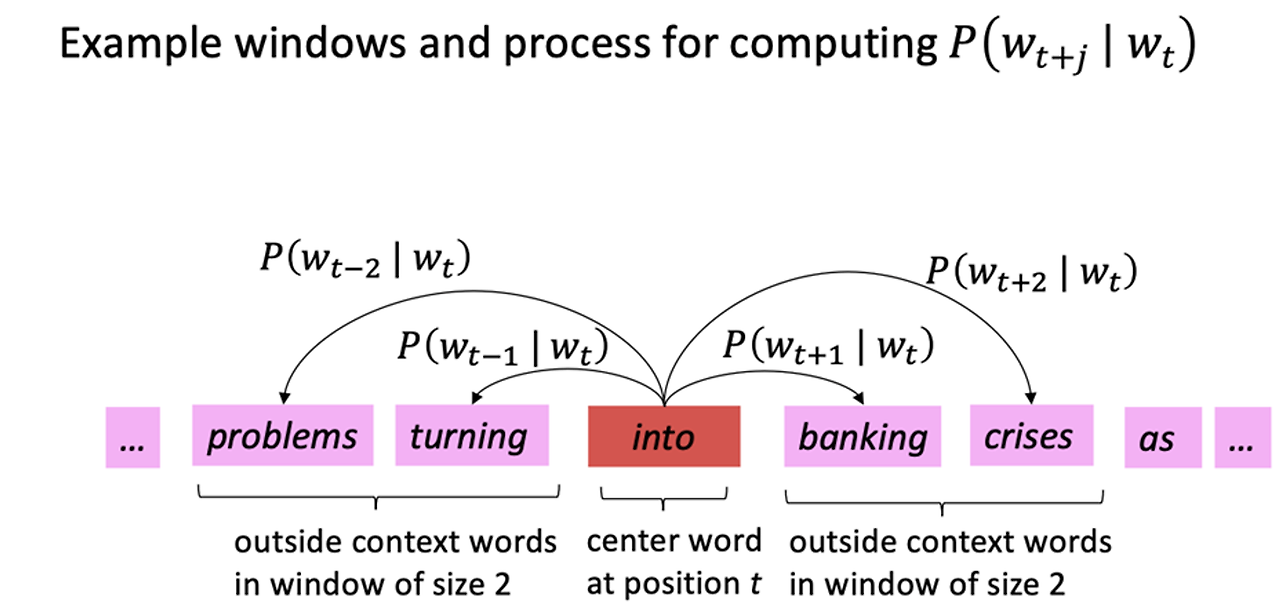
단어를 벡터로 변환하는 자연어 처리 기법 중 하나로, 단어의 의미적 유사성을 벡터 공간에서 나타내며, 신경망을 이용하여 단어 간의 관계를 학습
- 너무 큰 단어를 자른 고정 어휘를 선택하고, 희귀한 어휘를 제거한 큰 corpus 를 가진다
- corpus를 각 단어에 대한 벡터로 만들고 예상 단어와 예상 벡터를 생각한다.
ex) 앞뒤 단어 +-2를 확인하여 into가 나왔을 때 baking이 나올 확률 ... 등등을 계산
center word의 맥락에서 단어가 나타날 확률을 계산

corpus의 각 위치에 대해 중앙 단어 가 주어지면, 고정 크기 m의 window 내에서 문맥 단어를 예측
- 문맥에 나오는 단어들에 높은 확률을 부여하고자 한다.
- 다른 단어의 맥락에서 단어를 예측하는데, 얼마나 잘 수행할지에 대한 이전의 데이터 가능성이 무엇인지 알아내야함 ⇒
- 우도 L(θ): 텍스트 데이터에서 모델 파라미터 𝜃를 사용하여 중심 단어가 주어졌을 때 문맥 단어들이 나타날 확률
Word2Vec 목적 함수
우도 (Likelihood)
- 위치 t=1,…,T에 대해, 중심 단어 wt가 주어졌을 때 고정된 크기 m의 window 내에서 문맥 단어들을 예측하는 것이 목표
L(θ)=∏t=1T∏−m≤j≤mj≠0P(wt+j∣wt;θ)
- θ: 최적화해야 하는 모든 변수들
- wt: 중심 단어
- wt+j: 문맥 단어들
모델 파라미터 θ중, 중심 단어가 주어졌을 때 문맥 단어들을 관찰할 확률을 측정
목적 함수
목적 함수 J(θ)는 (평균) 음의 log 우도
J(θ)=−1TlogL(θ)=−1T∑t=1T∑−m≤j≤mj≠0logP(wt+j∣wt;θ)
- 확률의 곱을, 음의 로그로 변환하여 최적화를 쉽게 만듦.
- 모든 위치 t에 대해 평균을 구함으로써 목적 함수가 적절하게 스케일링 되도록 함. ( 음의 로그 우도의 평균)
- 최적화 문제에서 비용 함수로 사용
주요 포인트
- θ 최적화: 모델 학습을 최적화하는 것 = 문맥의 정확도를 최대화하는 것
- 최적화 L(θ)= 최적화 J(θ)
- Word2Vec라는 것은 학습시키는 동안J(θ) 를 최소화하는 파라미터 θ를 찾는 것임
- 이를 통해 중심 단어가 주어졌을 때 문맥 단어들을 올바르게 예측할 확률을 최대화
목표:
- 중심 단어 주변의 context word들의 가능성을 최대화해야함.
- 이를 위해 log likelihood 를 사용하여 합계로 변환
- 각 단어에 대한 벡터 표현을 가짐.
벡터 표현:
- 각 단어는 두 개의 벡터를 가진다.
확률 계산
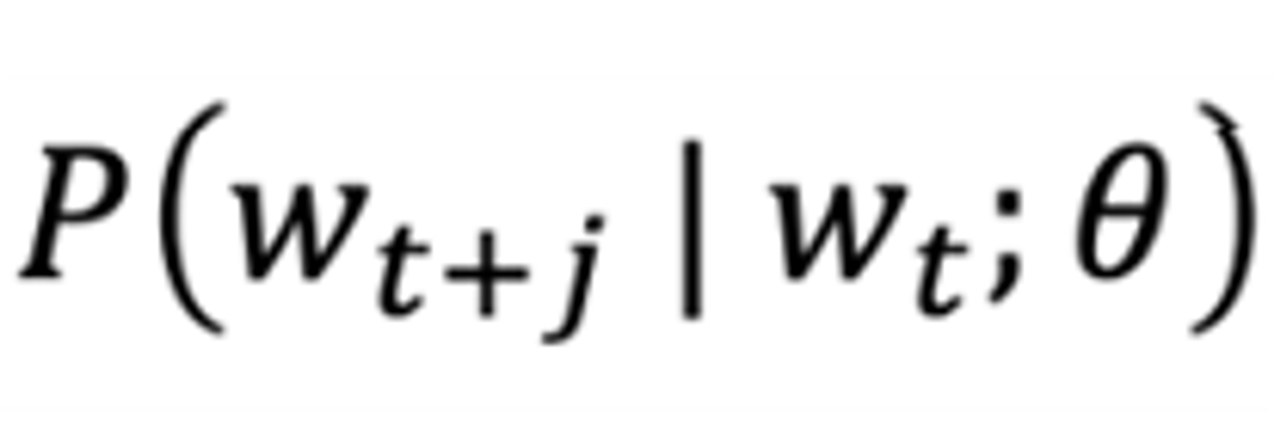
- center word가 C이고 context word가 O일 때, context word가 center 될 확률을 계산
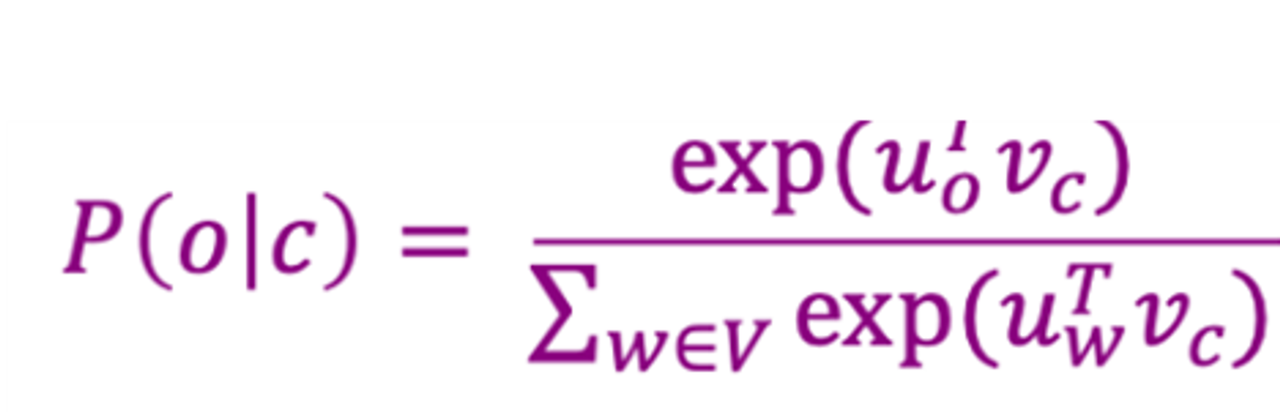
분자: 내적(Dot Product):
- 문맥 단어와 중심 단어의 임베딩 벡터 간의 내적을 계산
- 내적은 두 벡터의 유사성을 측정하는 방법
- 내적 값이 클수록 두 단어는 더 유사
- - 내적 값은 음수일 수 있지만, 확률은 음수가 될 수 없으므로 지수 함수(exponential function)를 사용하여 항상 양수 값을 만든다.
분모: 정규화(Normalization):
- 모든 단어에 대해 동일한 계산을 수행하여 확률 분포를 만든다.
- 분자 값을 전체 단어 집합(V)에 대해 계산된 값들의 합으로 나누어 정규화
- 이 과정은 전체 확률이 1이 되도록 보장
중요한 포인트
- 내적 값(Dot Product Value):
확률 분포
- 결과적으로,P(o∣c)는 o가 c일 확률을 나타냄.
- 이 확률은 항상 0과 1 사이의 값이 됨.
Softmax
- Softmax 함수는 입력값을 0과 1 사이의 확률 값으로 변환함.
- Softmax는 주어진 입력 값 xi를 확률 분포 pi로 변환하는 수식
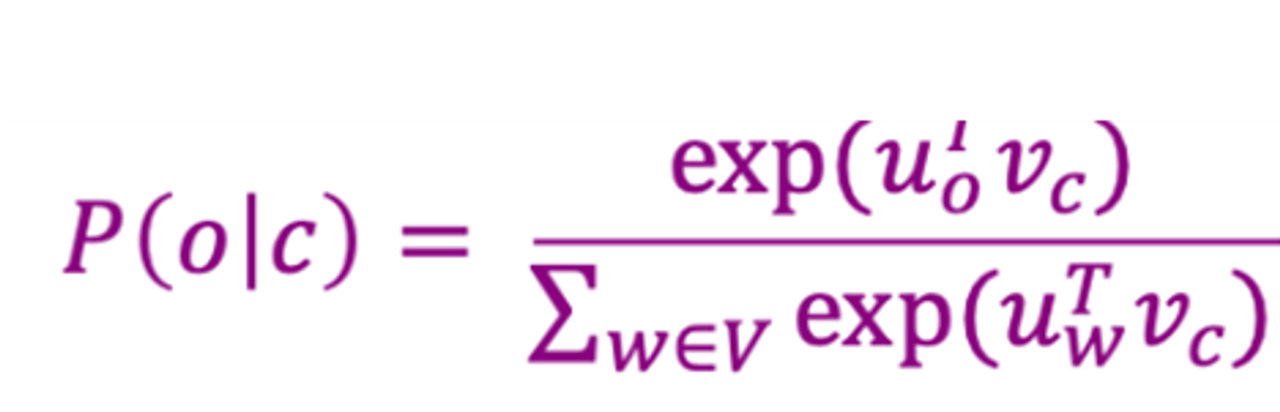

- input 벡터를 확률 벡터로 변환하고, 모든 확률의 합은 1이 됨.
- input 중 가장 큰 값의 확률을 증폭함("max").
- 또한 작은 값들에도 여전히 일부 확률을 할당함("soft").
Softmax 함수의 결과 = 확률분포
- 결과적으로 확률 분포가 나옴.
- 우리는 center의 맥락에서 실제로 단어의 확률을 최대화하여 단어 벡터를 생성함.
- 따라서 각 단어에 대해 context vector, center vector가 있음.
실제 벡터로 사용하려면
- 너무 많으니 우리는 미적분을 사용함.
- loss function 를 사용하여 도함수를 계산하고 gradient가 어디있는지 계산
- 내리막길이 무엇인지 파악하고 모델을 개선한다.
- 벡터 그래디언트를 계산하자.
# 데이터 세트에서 발견된 문자열이 무엇을 의미하는지 알 수 없는 이상한 문자열을 얻는 경향을 보임
model.most_similar(negative='banana')
# king, woman과 비슷하지만 man이 아닌 단어
result = model.most_similar(positive=['woman', 'king'], negative=['man'])
print("{}: {:.4f}".format(*result[0]))
# analogy 함수
def analogy(x1, x2, y1):
result = model.most_similar(positive=[y1, x2], negative=[x1])
return result[0][0]
# 예시 사용
analogy('man', 'king', 'queen') # 출력: queen
'CS224N' 카테고리의 다른 글
| [CS224N]Lecture 4 - Syntactic Structure and Dependency Parsing (0) | 2024.08.27 |
|---|---|
| [CS224N] Lecture 2 - Neural Classifiers - 신경망 분류 (0) | 2024.08.27 |
| [CS224N] Lecture 3 - Backprop and Neural Networks / 역전파, 순전파, 신경망 분류기 (0) | 2024.08.27 |