학습목표
(1) 신경망을 훈련시키기 위해 어떻게 수동으로 gradient를 계산할까
(2) back propagation(역전파 알고리즘)
~미리보기~
Back propagation:
계산 그래프(computation graph)를 따라 chain rule을 재귀적으로적용하는 과정 중 하나.
Forward Pass에서 저장한 중간 값을 사용하여, ouput Layer부터 input Layer 방향으로 기울기를 계산
이 기울기는 가중치 업데이트에 사용
Back propagation 에서의 기울기 계산은
[downstream gradient] = [upstream gradient] x [local gradient]
downstream gradient: 현재 노드의 기울기
upstream gradient: 이전(상류) 노드로부터 전달받은 기울기
local gradient: 현재 노드에서 계산된 기울기
---------------------------------------
Forward Pass
정의: 연산의 결과를 계산하고 중간 값을 저장하는 과정
입력 데이터를 각 층(layer)을 통해 전달하여 최종 출력을 계산
이 과정에서 각 층의 중간 출력 값을 저장
NER(Named Entity Recognition)이란?

사전에 없는 단어(패리스 힐튼 등) 가 있기 때문에 사전만의 단어로는 문장 해석을 해결할 순 없다.
context를 사용하여 이름을 가진 개체를 인식해야하는데, 신경망으로 이를 어떻게 해결할 수 있을까?
Simple NER: Window classification using binary logistic Classifier
- 각 단어를 이웃 단어들의 context winodw 안에서 분류
- 손으로 라벨링된 데이터를 사용하여 Logistic Classifier 훈련시켜서 각 클래스에 대해 중심단어 (YES/NO)로 분류하기 ⇒ 실제로는 다중 클래스 SOFTMAX를 사용하지만 강의에선 간단하게 ~
EX)
- 문맥 길이 2인 문장에서 "Paris"를 위치 기반으로 분류하기
- 문장: "the museums in Paris are amazing to see."

window 안의 단어 벡터들을 결합하여 입력 벡터를 만든다.
결과는

- To classifier all words: 모든 단어를 classifier하기 위해 문장의 각 단어에 대해 vector를 중심으로 classifier 실행.
NER: Binary classification for center word being location
- 손실 함수 Jt(θ)=σ(s)=11+e−8
단어의 위치 확률, σ는 sigmoid
- sigmoid는 negative sampling과 같은 logistic transform
- 점수 계산
- 은닉층 벡터 h
- 입력 벡터 x (5차원)
문맥 창에서 각 단어의 벡터들로 구성
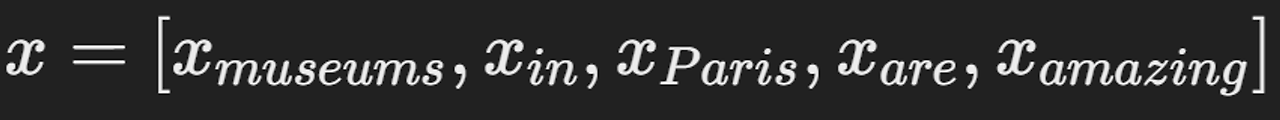
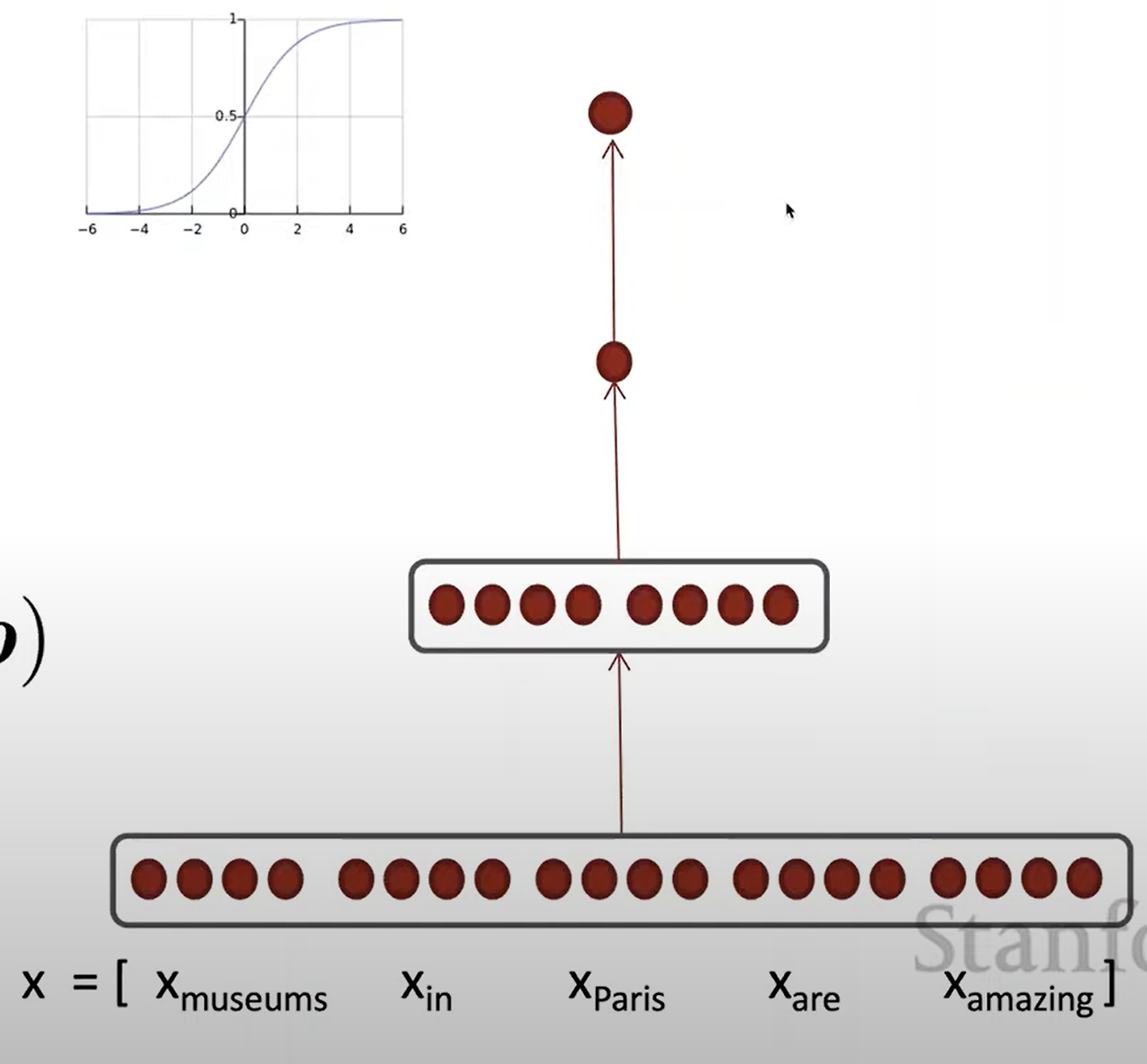
입력 벡터가 은닉층을 거쳐 최종 출력층으로 전달
손실 함수와 기울기 하강법
1이면 위치, 0이면 위치가 아님
- 그러나 실제로 Classifier는 0.9 와 같은 숫자를 return한다.
- 예측된 확률 값(0.9)과 실제 값(1 또는 0) 사이의 차이를 손실 함수로 계산
이 경우 거리 공식 사용
- Loss=(예측값−실제값)2
기울기 하강법을 사용하여 파라미터를 업데이트 (손실을 줄이기 위해 파라미터를 조정)

- θ는 손실 함수의 기울기 방향의 반대 방향으로 조정 - θ는 파라미터, α: 학습률, ∇θLoss: 손실 함수의 기울기
Gradient Computing
- Matrix calculus(행렬 미적분)
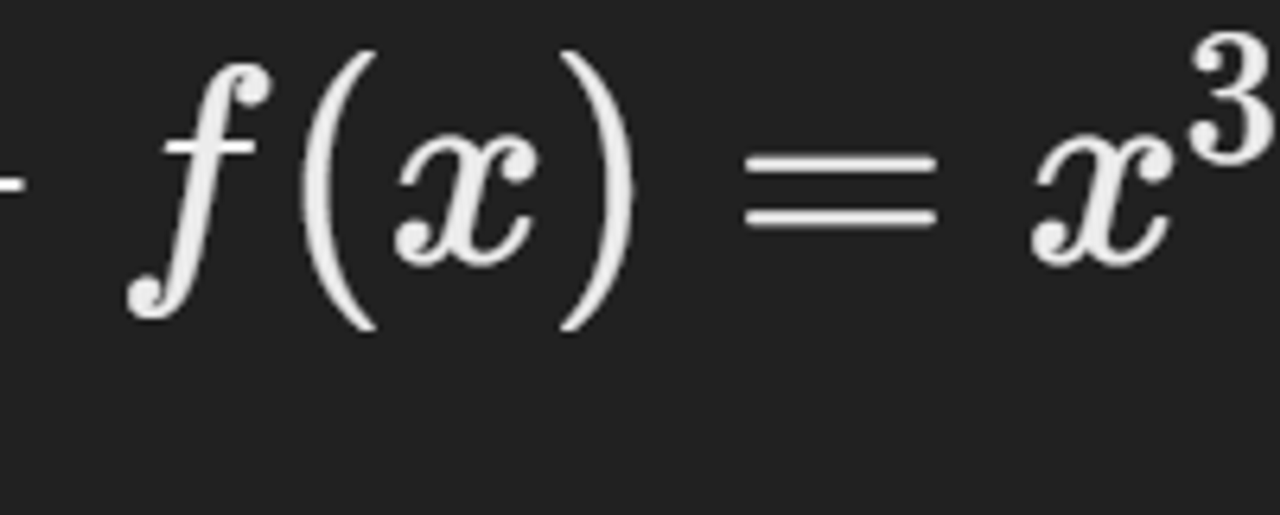
- 기울기
입력값 x에서의 작은 변화가 출력값에 미치는 영향을 도함수를 통해 알 수 있음
입력의 작은 변화가 출력에 미치는 영향
x=1일 때.
변화량≈3×(입력의작은변화)
- x=1 에서 작은 변화를 주면 출력은 약 3배.
- 예를 들어, x=1에서 1.01로 변경하면, 1.013≈1.03
x=4일 때.
변화량≈48×(입력의작은변화)
x=4 에서 작은 변화를 주면 출력은 약 48배.
- 예를 들어, x=4에서 4.01로 변경하면, 4.013≈64.48
- 함수 정의
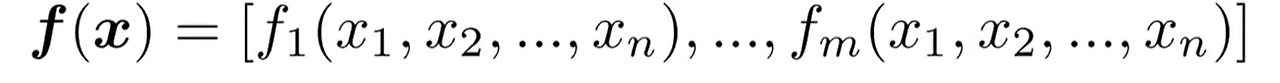
input : n개
output: 1개
- 기울기 벡터(gradient):
함수의 기울기는 각 입력에 대한 편미분(partial derivatives)로 구성된 vector
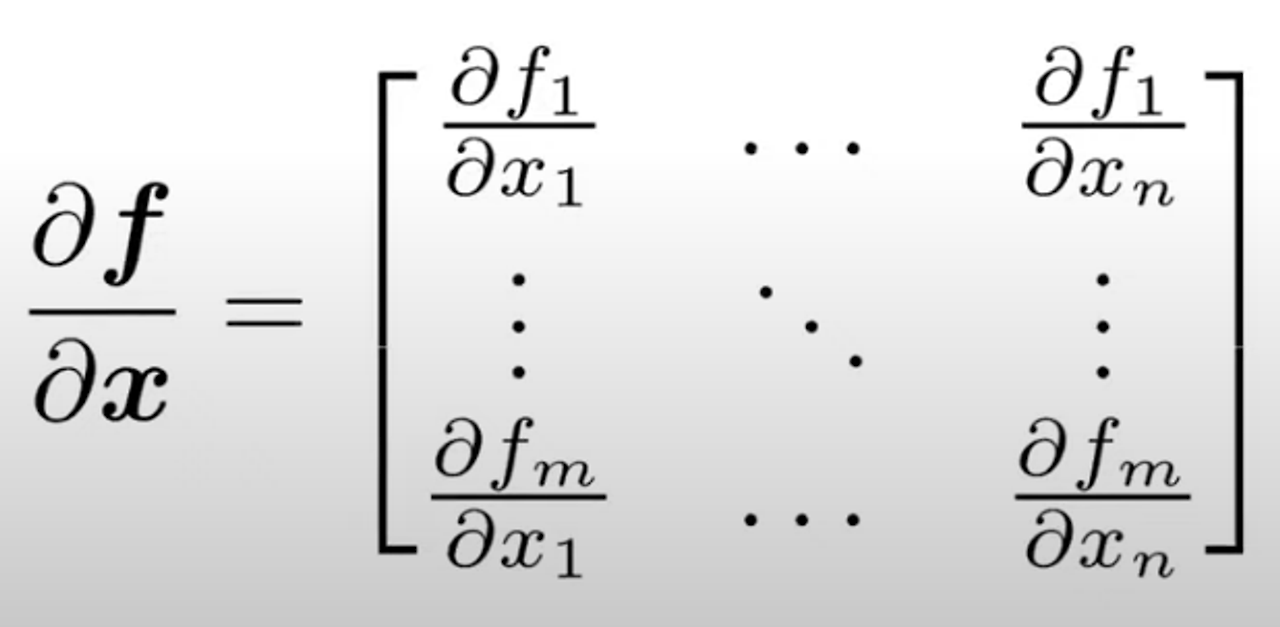
기울기 벡터는 함수 f의 각 입력 변수에 대한 편미분으로 구성
각 요소는 하나의 변수에 대한 함수의 단순 미분처럼 계산
이를 각각의 input으로 편미분하면

신경망에서의 적용
- 신경망에서 사용하는 기울기는 각 층의 가중치와 편향에 대한 편미분으로 구성
- 학습 과정에서 Back propagation 를 통해 계산
Neural Networks 에서 Back propagation(역전파) 를 통해 기울기를 계산하기
Chain Rule
복합 함수의 미분을 계산하는 방법으로, 역전파 과정에서 사용
각 노드에서의 gradient 는 해당 노드의 output gradient와 gradient에 대한 미분을 곱하여 계산
- 두 함수의 합성에서 미분을 계산
- 두 함수의 도함수를 곱하는 것
- one - variable function Multiply derivatives

chain rule 적용
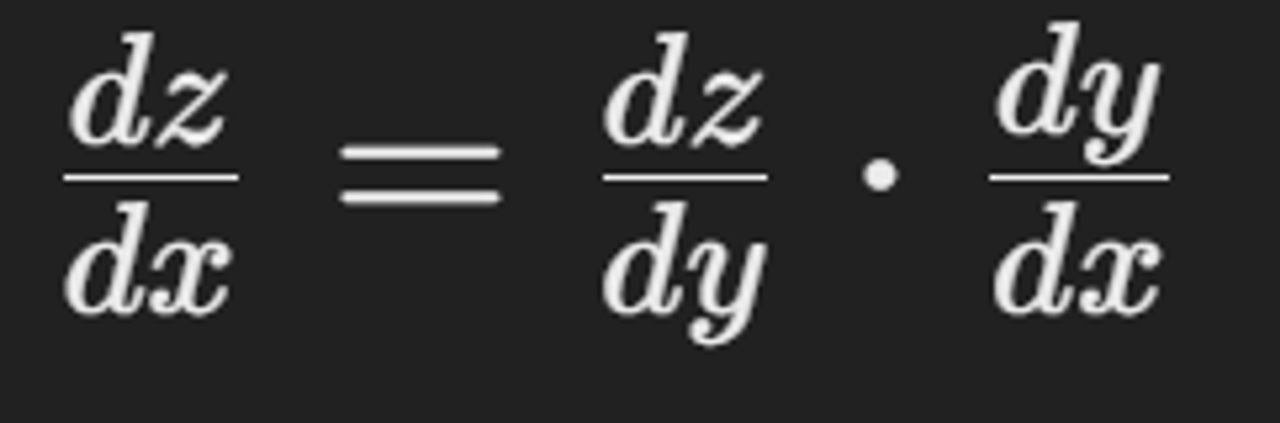
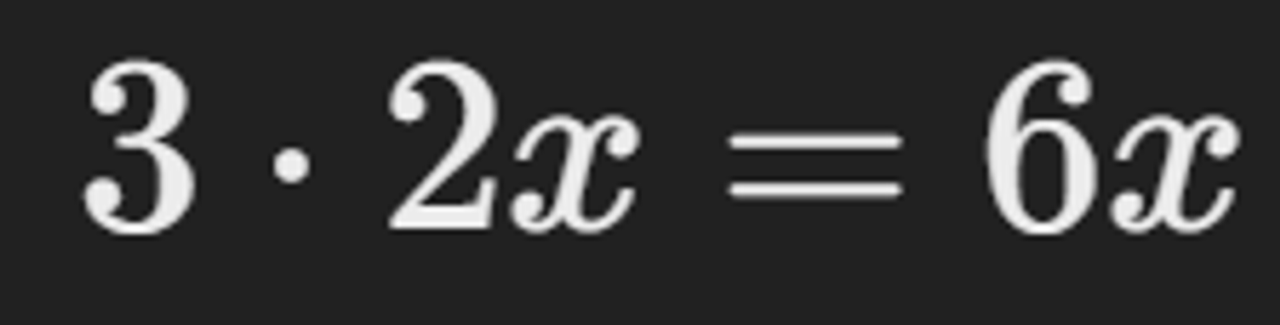
벡터와 행렬의 경우
- Jacobian martrix 사용
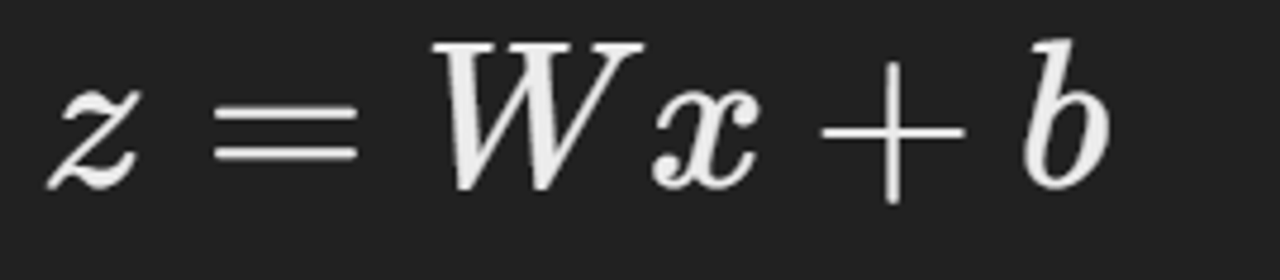
w: 행렬, x: 입력 벡터, b: 편향 벡터
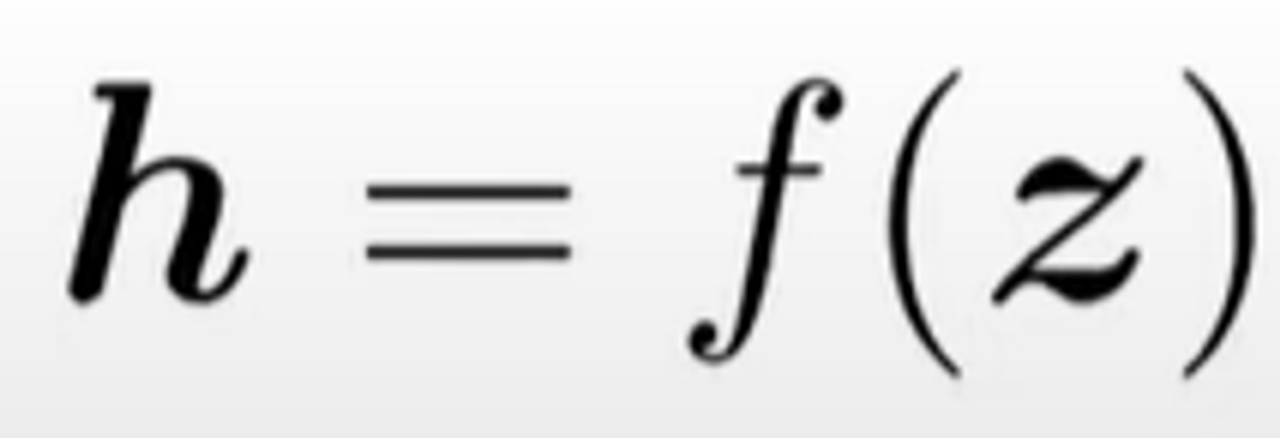
비선형 활성화 함수 f를 적용
- chain rule 적용
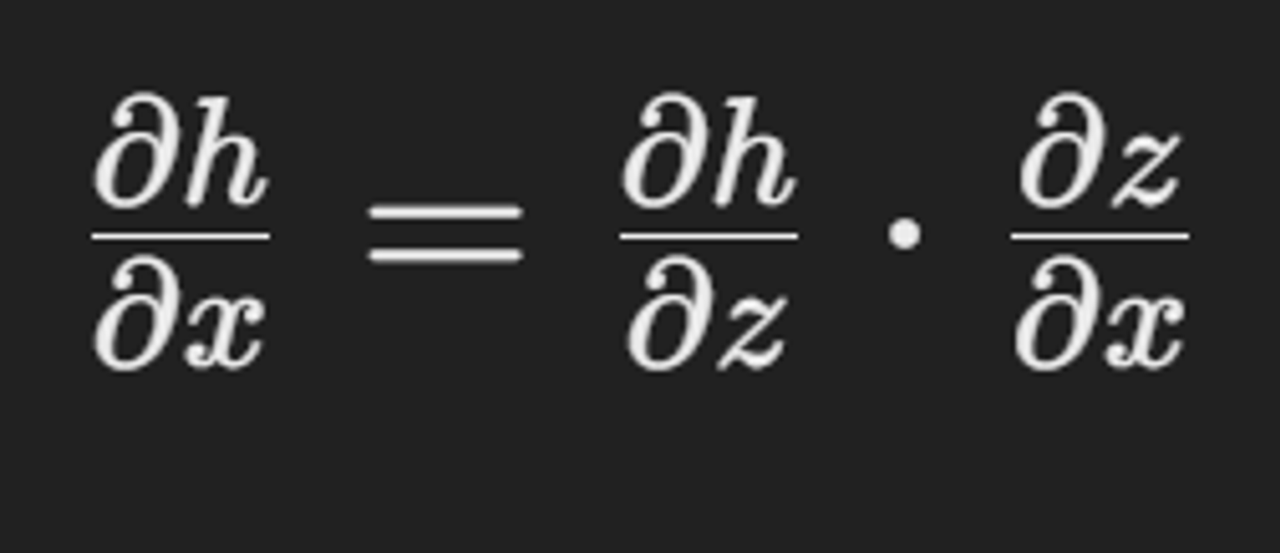
h에 대한 x의 편미분
h에 대한 z의 편미분 * x의 편미분
- jacobian martix
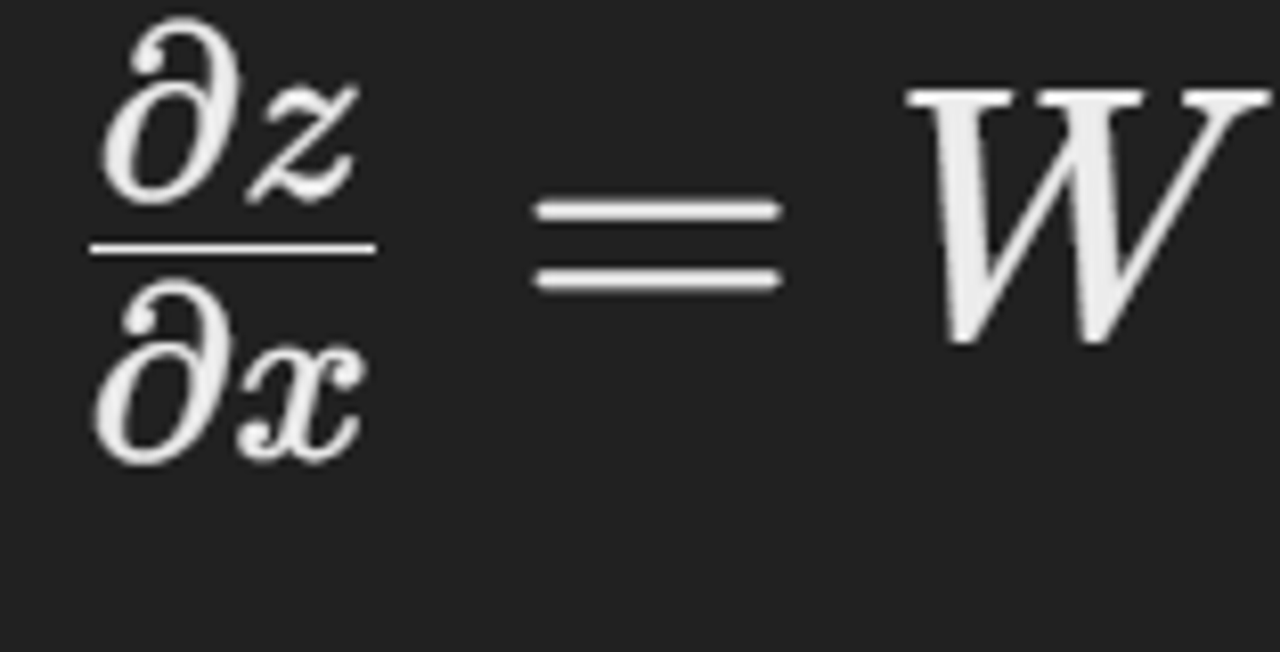
z=Wx+b이므로 W는 상수 행렬
Nonlinearities(비선형성)
- Jacobian Elementwise activation Function
- 활성화 함수와 벡터
비선형성을 도입하기 위해 벡터를 활성화 함수 f (예: 시그모이드 함수)에 통과
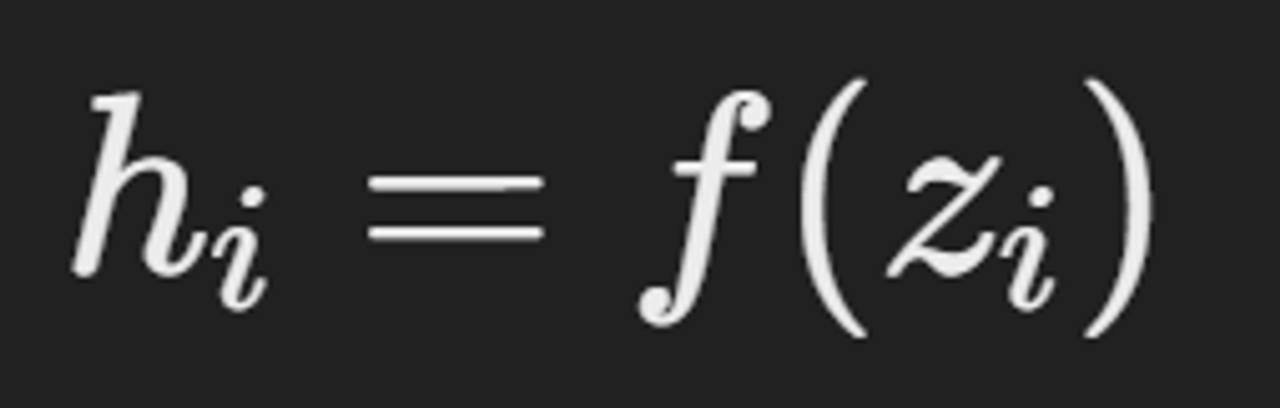

- Jacobian 행렬 정의
h에 대한 z의 Jacobian 행렬은 각 출력 hi에 대한 각 입력 zj의 편미분으로 구성

- 요소별 편미분
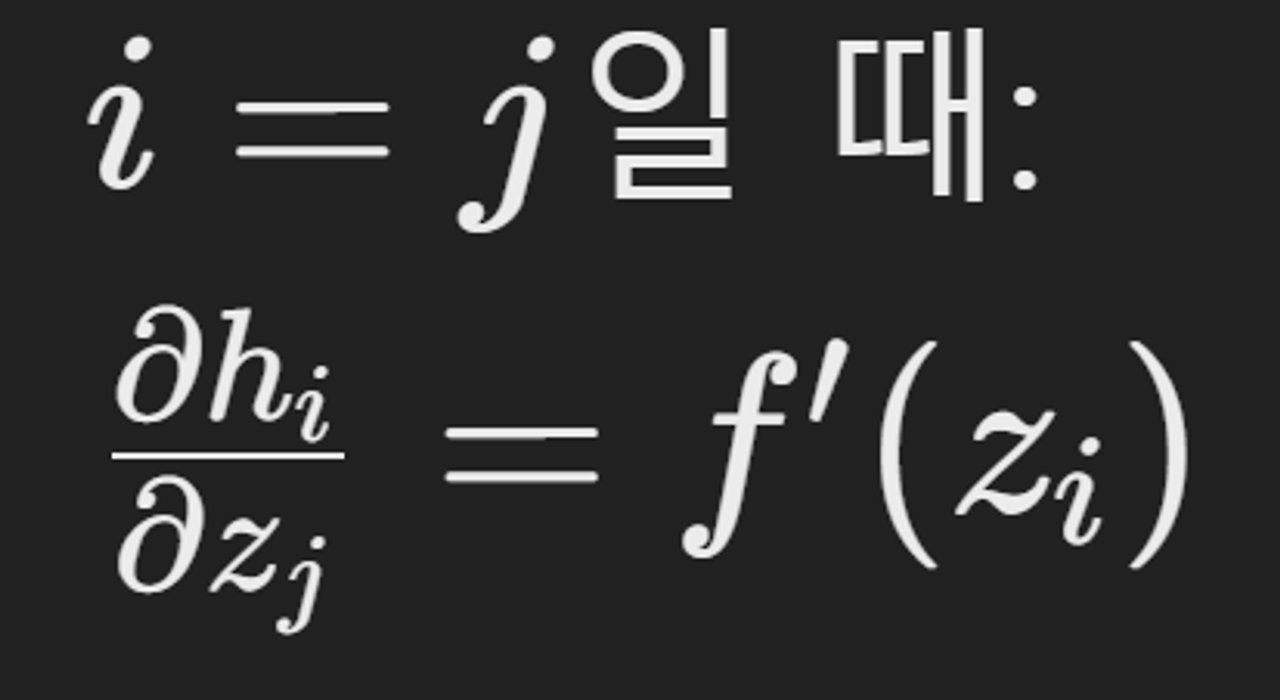
로지스틱 함수의 단변수 미분을 얻게 된

입력이 출력에 영향을 미치지 않으므로 0을 얻는다.
- diagonal matrix (대각 행렬)구성 ⇒ 도함수가 대각선에 있음
대각선 요소: f′(zi) 로 구성
나머지 요소: 0

Jacobians
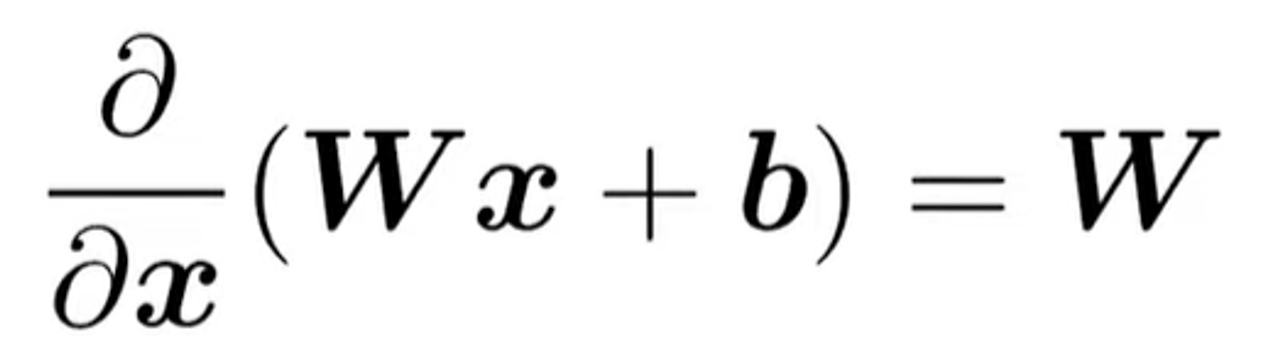
- Wx+b를 x에 대해 편미분
W: 가중치 행렬, x: 입력 벡터, b: 편향 벡터
⇒ 결과적으로, x에 대한 편미분은 행렬 W
이는 단변수 미적분에서 ax+b를 x에 대해 미분하면 a가 되는 것과 유사
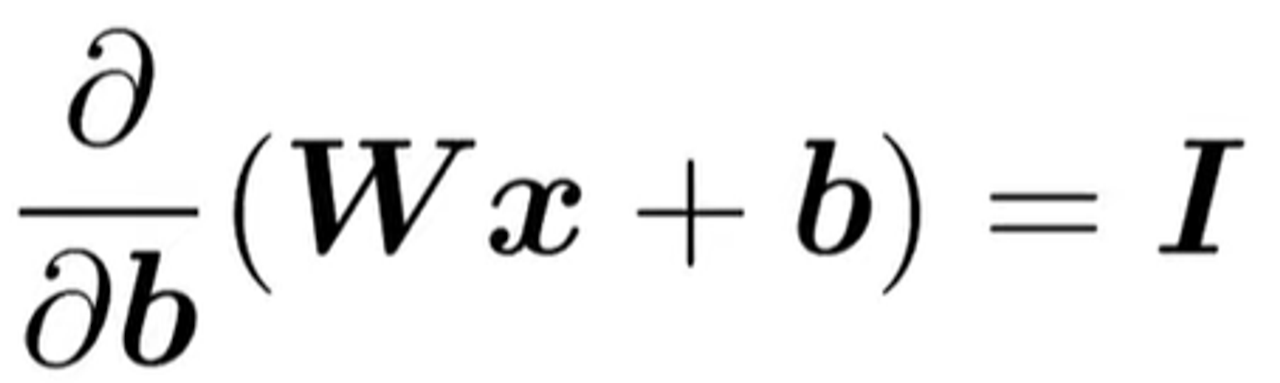
- Wx+b를 b에 대해 편미분
- 이는 단변수 미적분에서 상수 항을 미분하면 1이 되는 것과 유사

u와 h의 내적 uTh를 u에 대해 편미분
u와 h: vector u에 대한 편미분은 h의 전치 행렬 hT
역전파 계산
원래는 손실함수 Jt를 계산해야 하지만, 간단하게 score함수의 gradient를 계산
(1) 식을 단순화하기
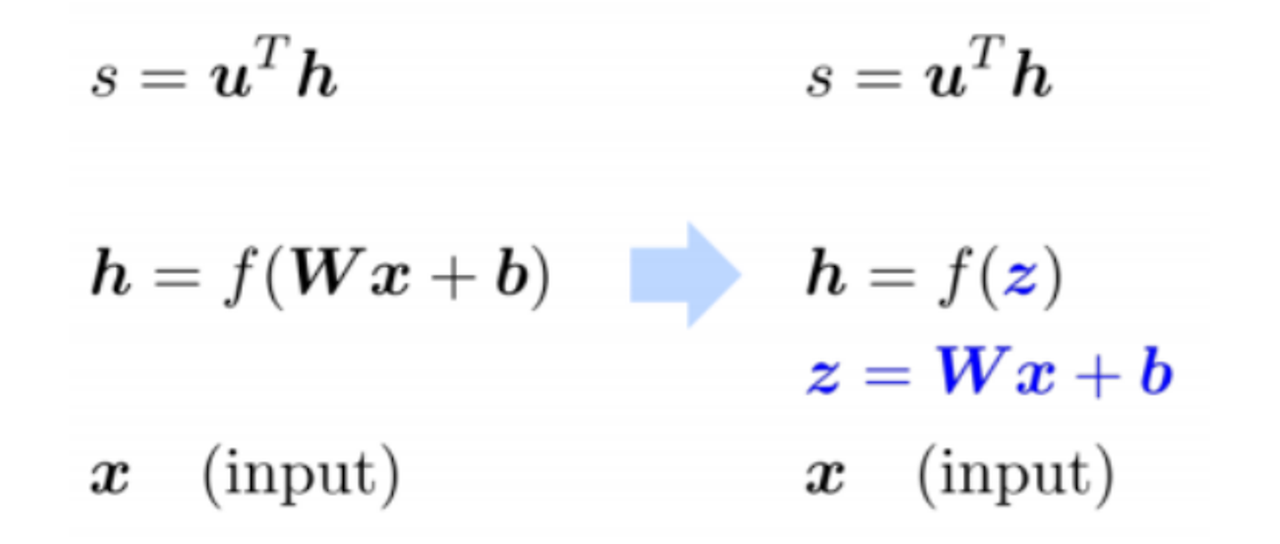
z = Wx + b로 치환
(2) Jacobian 행렬 작성하기

(1) s를 h로 미분
(2) h를 z로 미분
(3) z를 b로 미분
모두 곱하면 최종적으로 s를 b로 미분한 값

Jacobians 헤더 확인
결과
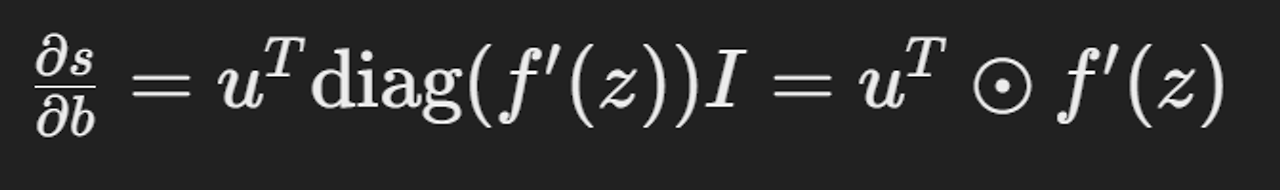

모든 파라미터에 대해서 역전파를 수행하여 파라미터 값들을 업데이트해야함.
W에 대해 미분: S를 w로 미분하면…?


파란색: 델타
델타는 오류 신호. 편도함수를 계산하는 매개변수
델타 값은 한 번만 계산하여 효율성을 증가
Shape Convention

- 행렬 W= n×m 형태
- 행렬 W의 모든 요소에 대한 n x m개의 요소를 가진
1×nm 형태의 Jacobian martrix 생성
그러나,

해당 식을 계산하기 힘듬 ⇒ 실제로 기울기의 형상은 매개변수의 형상과 동일하게 유지하는 것이 편리
따라서,
∂s∂W=n∗m
δ: Local error signal ∂s∂z
x: local input signal
z = Wx + b이므로,



38분
흠 왜 세타에 T제곱일까
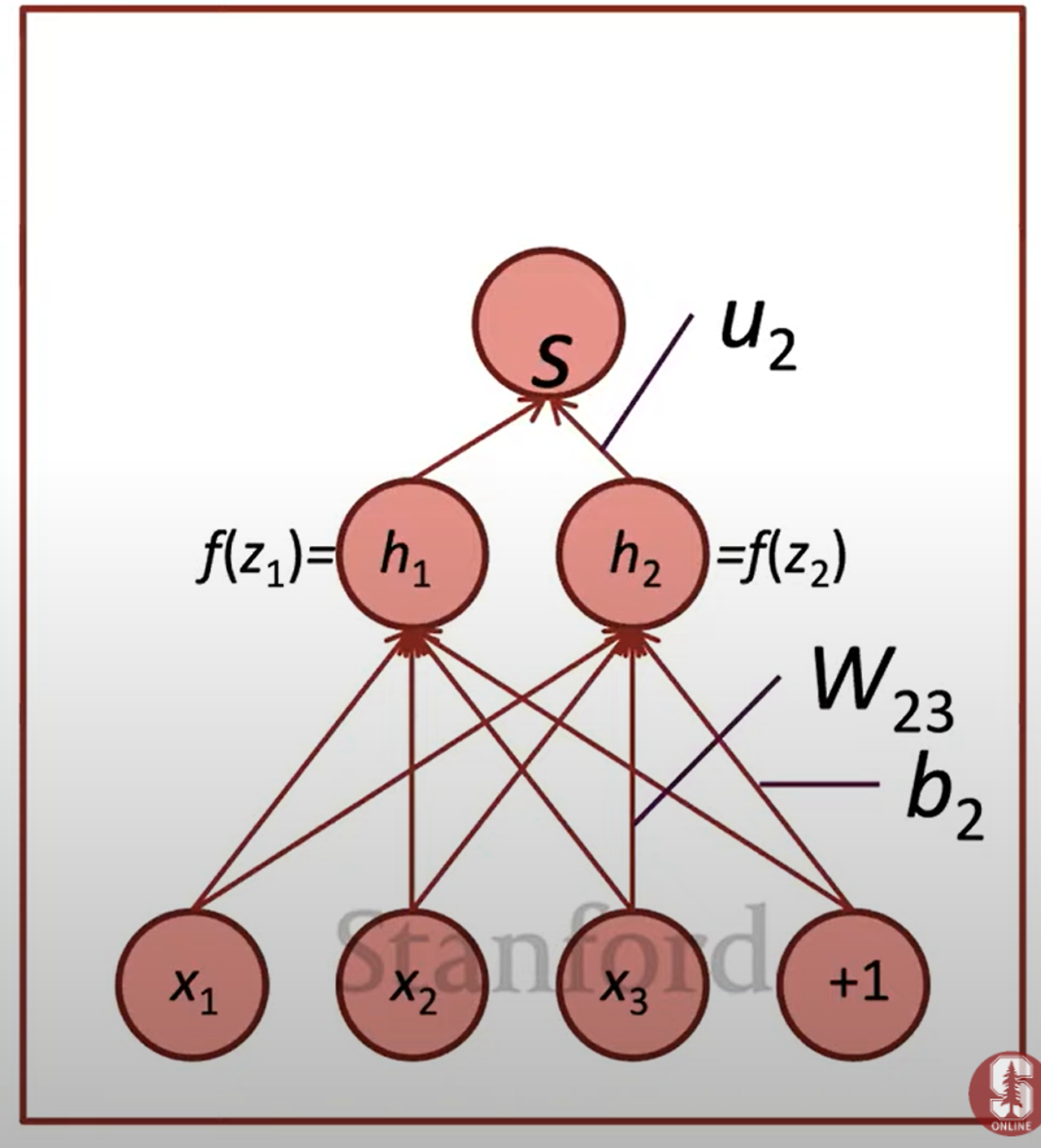

그림 예시에서, W23은 z3에만 기여
z1은 신경도 안 씀
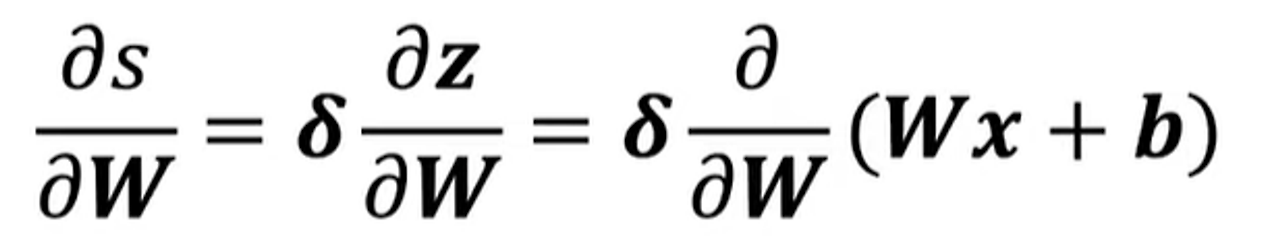
- 편미분 계산하기
zi의Wij에대한편미분을계산할때,
Wij⋅xij+bi형태가 됨

의 모든 항에 대해 Wij를 편미분할 때,
Wij가 포함된 항 빼고
전~부 모든 항의 편미분은 0
따라서, Wij에 대한 편미분은 xj
항의 편미분 a에 대한 ax의 편미분과 같음
답은 Xj
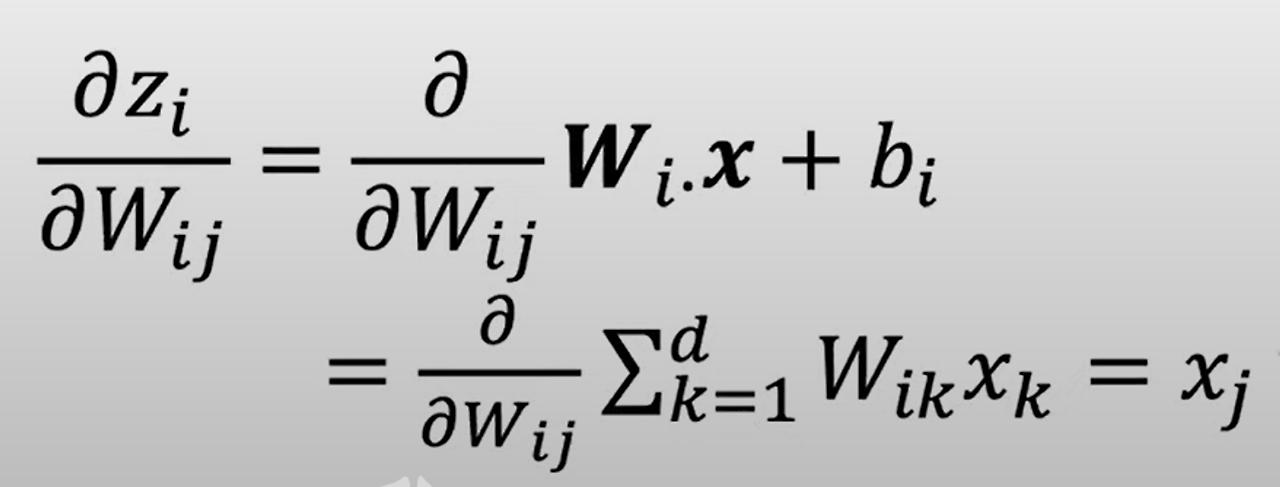
왜 신경망의 기울기를 계산할 때 transpose (전치행렬)을 사용하나?

- 차원 맞추기

- 결과 행렬

이렇게 하면 차원이 맞아 떨어진다
입력의 각 요소가 출력의 각 요소로 가는 방식에서
외적 행렬을 얻기 위해 형상 규칙을 사용
Jacobian vs Shape Convention

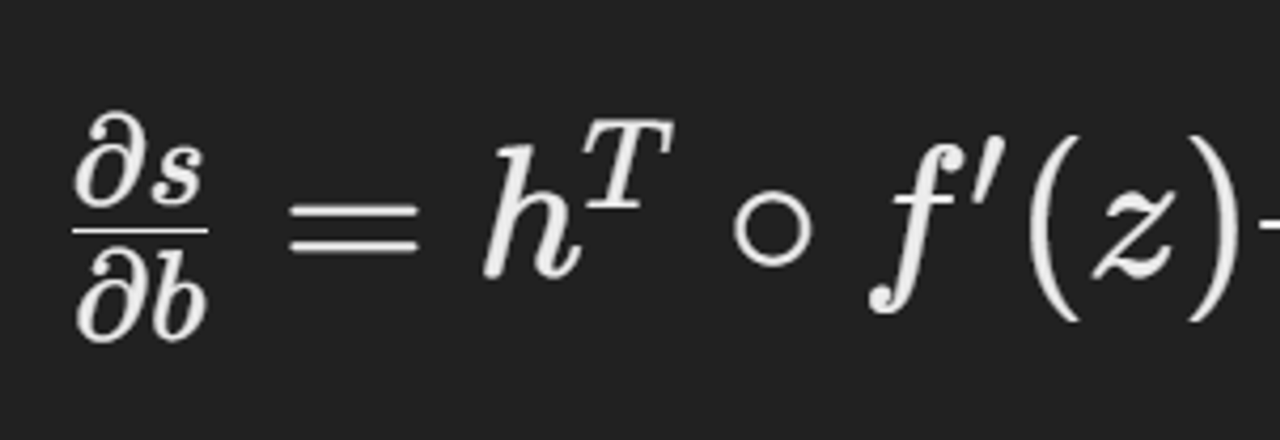
위의 식은 row vector이다
- 하지만, shape convention에 따르면, gradient는 column vector이어야한다.
- b가 column vector이기 때문
Jacobian vs Shape Convention
jacobian: 미분 계산이 쉽다
shape convention: SGD Stochastic Gradient Descent 구현이 유용
⇒ 기울기가 행렬과 같은 shape이므로, 기울기 업데이트가 쉬움
기울기 업데이트를 할 때 계산의 일관성을 유지할 수 있음.
그러나 실제로는 두 가지 모두 필요함
- 과제는 shape covention으로~!

신경망에서 기울기를 계산할 때 어떤 형식을 따를까
1) Jacobian 형식을 최대한 사용한 후, 마지막에 Shape Convention

2) Always Shape Convention

- 조금 더 해킹적일 수 있지만, 차원을 맞추기 위해 언제 transpose하거나 reshape해야 하는지 확인
- 하지만 Gradien Shape이 항상 파라미터의 Shape과 같아야 함
- θ( 오차 메시지) 가 항상 해당 은닉층과 같은 차원을 가진다는 점을 사용해 해결할 수 있음.
⇒ 뉴런 수와 같은 차원. 은닉층에 5개의 뉴런이 있다면, θθ도 5차원 벡터
Back propagation
미분을 취하고 (일반화된, 다변수, 혹은 행렬 Chain Rule을 사용하는 것
계산을 최소화하기 위해 상위 층에서 계산된 미분을 하위 층의 미분 계산에 재사용하는 것
Computation Graph

계산 그래프는 신경망의 연산을 tree 형태로 표현하며, 일반적인 경우에는 방향성 그래프로 나타낸다


- 순전파 한 후, 화살표의 방향, gradient을 반대로 바꿔서 역전파를 진행
- b, W, u와 같은 다양한 파라미터에 대해 gradient 를 전달.
- 이런 그래디언트를 사용하여 stochastic gradient descent을 통해 b와 W의 값을 변경
- 순전파와 역전파를 반복하며 신경망 학습 진행
------------------------------------------------------------------------------------------------
Forward Propagation (순전파)
- 주어진 입력값을 통해 연산을 순차적으로 진행하여 최종 출력값을 구하는 과정
- 컴파일러가 수식을 계산하는 방식과 유사
Back propagation (역전파)
- 계산 그래프를 통해 gradient를 역방향으로 전파하여 모델의 매개변수들을 업데이트하는 과정
- 손실 함수의 기울기를 계산하고 매개변수를 업데이트하여 손실을 최소화하는 역할을 한다.
- 순전파 (Forward Propagation):
- 역전파 (Backpropagation):
'CS224N' 카테고리의 다른 글
| [CS22SN] 우리는 왜 NLP가 필요할까? / Lecture 1 - Intro & Word Vectors (1) | 2024.08.27 |
|---|---|
| [CS224N]Lecture 4 - Syntactic Structure and Dependency Parsing (0) | 2024.08.27 |
| [CS224N] Lecture 2 - Neural Classifiers - 신경망 분류 (0) | 2024.08.27 |